Skillnad mellan rektangel och rhombus: rektangel vs rhombus

Rektangel vs Rhombus

Rhombus och rektangel är fyrhjulingar. Geometrin hos dessa figurer var känd för människan i tusentals år. Ämnet behandlas uttryckligen i boken "Elements" som skrivits av grekisk matematiker Euclid.

Parallelogram

Parallelogram kan definieras som den geometriska figuren med fyra sidor, med motsatta sidor parallella med varandra. Mer precist är det en fyrkant med två par parallella sidor. Denna parallella karaktär ger många geometriska egenskaper till parallellogrammen.

En fyrsidig är ett parallellogram om följande geometriska egenskaper finns.

• Två par motstående sidor är lika långa. (AB = DC, AD = BC)

• Två par motsatta vinklar är lika stora. (

)

• Om de intilliggande vinklarna är kompletterande

• Ett par sidor som är motsatta varandra är parallella och lika långa. (AB = DC & ABindDC)

• Diagonalerna halverar varandra (AO = OC, BO = OD)

• Varje diagonal delar fyrsidan i två kongruente trianglar. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

Vidare är summan av sidans kvadrater lika med summan av kvadraterna av diagonalerna. Detta kallas ibland som parallellogramlag och har utbrett applikationer inom fysik och teknik. (AB ² + BC ² + CD ² + DA ² = AC ² + BD ² )

Var och en av ovanstående egenskaper kan användas som egenskaper, när det väl har fastställts att fyrsidan är ett parallellogram.

Parallellogrammets område kan beräknas med produkten av längden på en sida och höjden till motsatt sida. Därför kan parallellogrammets område anges som

Area of ​​parallelogram = bas × height = AB × h

Parallellogrammets område är oberoende av formen av det enskilda parallellogrammet. Det är endast beroende av längden på basen och den vinkelräta höjden.

Om sidorna av ett parallellogram kan representeras av två vektorer kan området erhållas med storleken av vektorprodukten (tvärprodukt) hos de två intilliggande vektorerna.

Om sidor AB och AD representeras av vektorerna (

) respektive (

), anges området för parallellogrammet med

, där α är vinkeln mellan

och.

Följande är några avancerade egenskaper hos parallellogrammet;

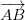
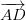
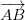
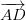
• Området med ett parallellogram är dubbelt så stor som en triangel som skapas av någon av dess diagonaler.

• Parallellogrammets område är uppdelad i hälften av varje linje som passerar genom mittpunkten.

• En icke-degenererad affine-transformation tar ett parallellogram till ett annat parallellogram.

• Ett parallellogram har rotationssymmetri i ordning 2

• Summan av avstånden från varje inre punkt i ett parallellogram till sidorna är oberoende av Platsen för punkten

Rektangel

En fyrkantig med fyra rät vinklar kallas en rektangel. Det är ett speciellt fall av parallellogrammet där vinklarna mellan två intilliggande sidor är rätvinkliga.

Förutom alla egenskaperna hos ett parallellogram kan ytterligare egenskaper igenkännas när man beaktar rektangelens geometri.

• Varje vinkel i vinklarna är rätt vinkel.

• Diagonalerna är lika långa och de halverar varandra. Därför är de bisected sektionerna lika långa.

• Diagonalernas längd kan beräknas med Pythagoras teorem:

PQ

2 ^{+ PS} 2 ^{= SQ} 2 ^{• Områdesformeln minskar till produkten av längd och bredd.}

Rektangelarea = längd × bredd

• Många symmetriska egenskaper finns på en rektangel, t.ex.

- En rektangel är cyklisk, där alla hörn kan placeras på omkretsens omkrets.

- Det är equiangular, där alla vinklarna är lika.

- Det är isogonalt, där alla hörn ligger inom samma symmetriska omloppsbana.

- Den har både reflektionssymmetri och rotationssymmetri.

Rhombus

En fyrsidig med alla sidor är lika långa är känd som en rhombus. Den heter även som en

jämviktsfyra sida . Det anses ha en diamantform, som liknar den i spelkorten. Rhombus är också ett speciellt fall av parallellogrammet. Det kan betraktas som ett parallellogram med alla fyra sidor lika. Och det har följande speciella egenskaper, förutom egenskaperna hos ett parallellogram.

• Rhombos diagonaler halverar varandra i rät vinkel; diagonalerna är vinkelräta.

• Diagonalerna tvingar de två motsatta inre vinklarna.

• Minst två av de intilliggande sidorna är lika långa.

Rhombusens område kan beräknas i samma metod som parallellogrammet.

Vad är skillnaden mellan Rhombus och Rectangle?

• Rhombus och rektangel är fyrhjulingar. Rektangel och rhombus är speciella fall av parallellogrammen.

• En yta kan beräknas med formeln

bas × höjd . • Med tanke på diagonalerna;

- Rhombusens diagonaler halverar varandra i rät vinkel och de bildade trianglarna är liksidiga.

- Rektangelens diagonaler är lika långa och halverar varandra. bisektionerna är lika långa. Diagonalerna halverar rektangeln i två kongruenta högra trianglar.

• Med tanke på de interna vinklarna;

- Rhombusens inre vinklar är bisected av diagonalerna

- Alla fyra inre vinklarna av rektangeln är rätvinkliga.

• Med tanke på sidorna;

- Eftersom alla fyra sidorna är lika i en rhombus är fyra gånger en kvadrat av en sida lika med summan av kvadraterna av diagonalen (med Parallelogram Law)

- I rektanglar är summan av rutorna av de två intilliggande sidorna är lika med kvadraten av diagonalen vid ändarna.(Pythagoras regel)