Skillnad mellan parallellogram och fyrsidor: parallellogram mot fyrsidig
Parallelogram vs fyrsidig < Fyrhjulingar och parallellogram är polygoner som finns i Euklidisk geometri. Parallelogram är ett speciellt fall av fyrsidan. Fyrhjulingar kan vara antingen plana (2D) eller 3-dimensionella medan parallellogram är alltid plana.
Fyrsidan
Fyrsidan är en polygon med fyra sidor. Den har fyra vertikaler, och summan av de inre vinklarna är 3600 (2π rad). Fyrhjulingar klassificeras i självkorsande och enkla fyrsidiga kategorier. De självkorsande fyrhjulederna har två eller flera sidor som korsar varandra, och mindre geometriska figurer (som trianglar bildas inuti fyrsidan).
De enkla kvadrilateralerna är också uppdelade i konvexa och konkava fyrhjulingar. Konkave fyrhjulingar har intilliggande sidor bildande reflexvinklar inuti figuren. De enkla fyrhjulederna som inte har reflexvinklar invändigt är konvexa fyrhjulingar. De konvexa fyrsidorna kan alltid ha tessellationer.

Parallelogram kan definieras som den geometriska figuren med fyra sidor, med motsatta sidor parallella med varandra. Mer precist är det en fyrkant med två par parallella sidor. Denna parallella karaktär ger många geometriska egenskaper till parallellogrammen.
En fyrsidig är ett parallellogram om följande geometriska egenskaper finns.

• Två par motstående sidor är lika långa. (AB = DC, AD = BC)
• Två par motsatta vinklar är lika stora. ()

• Ett par sidor som är motsatta varandra är parallella och lika långa. (AB = DC & AB|DD)
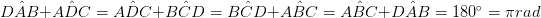
• Diagonalerna halverar varandra (AO = OC, BO = OD)
• Varje diagonal delar fyrsidan i två kongruente trianglar. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)
Vidare är summan av sidans kvadrater lika med summan av kvadraterna av diagonalerna. Detta kallas ibland som
parallellogramlag och har utbrett applikationer inom fysik och teknik. (AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + BD 2 ) Var och en av ovanstående egenskaper kan användas som egenskaper, när det väl har fastställts att fyrsidan är ett parallellogram.
Parallellogrammets område kan beräknas med produkten av längden på en sida och höjden till motsatt sida. Därför kan parallellogrammets område anges som
Area of parallelogram = bas × height =
AB × h Parallellogrammets område är oberoende av formen av det enskilda parallellogrammet. Det är endast beroende av längden på basen och den vinkelräta höjden.

Om sidorna av ett parallellogram kan representeras av två vektorer kan området erhållas med storleken av vektorprodukten (tvärprodukt) hos de två intilliggande vektorerna.
Om sidor AB och AD representeras av vektorerna () respektive (





• Parallellogrammets område är uppdelad i hälften av varje linje som passerar genom mittpunkten.
• En icke-degenererad affine-transformation tar ett parallellogram till ett annat parallellogram.
• Ett parallellogram har rotationssymmetri i ordning 2
• Summan av avstånden från varje inre punkt i ett parallellogram till sidorna är oberoende av Placeringen av punkten
Vad är skillnaden mellan Parallelogram och Fyrhjuling?
• Fyrkantiga sidor är polygoner med fyra sidor (ibland kallade tetragoner) medan parallellogram är en speciell typ av en fyrsidig.
• Quadrilaterals kan ha sina sidor i olika plan (i 3D-rymden) medan alla sidor av parallellogrammet ligger på samma plan (plan / 2dimensional).
• Fyrkantens invändiga vinklar kan ta något värde (inklusive reflexvinklar) så att de lägger till 3600. Parallelogram kan bara ha obtuse vinklar som maximal vinkel.
• Fyra sidor av fyrsidan kan ha olika längder medan parallellogrammets motsatta sidor är parallella med varandra och lika långa.
• Varje diagonal delar parallellogrammet i två kongruente trianglar, medan trianglarna som bildas av diagonalen i en allmän fyrkant inte nödvändigtvis är kongruenta.