Skillnad mellan derivat och differential

Derivat vs Differential

I differentialkalkylen är derivat och differentiering av en funktion nära besläktade men har mycket olika betydelser, och brukade representera två viktiga matematiska objekt relaterade till differentierbara funktioner.

Vad är derivat?

Derivat av en funktion mäter den takt vid vilken funktionsvärdet ändras som inmatningsändringar. I flera variabla funktioner beror ändringen i funktionsvärdet på riktningen för förändringen av värdena för de oberoende variablerna. Därför väljs en specifik riktning i sådana fall och funktionen differentieras i den specifika riktningen. Det här derivatet kallas riktningsderivatet. Partiella derivat är en speciell typ av riktningsderivat.

Derivat av en vektorvärderad funktion f kan definieras som gränsen

varhelst den existerar. Som nämnts tidigare ger detta oss ökningstakten av funktionen f längs vektorns riktning u. I fallet med en värderingsfunktion reduceras detta till den välkända definitionen av derivatet,

Till exempel är

överallt differentierbar, och derivatet är lika med gränsen,

, som är lika med

. Derivaten av funktioner som

finns överallt. De är lika med funktionerna

Detta är känt som det första derivatet. Vanligtvis anges det första derivatet av funktionen f av f ⁽¹⁾ . Nu med den här notationen är det möjligt att definiera högre orderderivat.

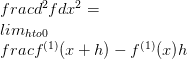
är det andra ordningsriktningsderivatet och betecknar n ^th derivatet med f ⁽ⁿ⁾ för varje n,

, definierar n ^th derivatet.

Vad är differential?

Differensial för en funktion representerar förändringen i funktionen med avseende på förändringar i den oberoende variabeln eller variablerna. I den vanliga notationen är den totala differensen av order 1 df givet av för en given funktion f av en enda variabel x

. Detta betyder att för en oändlig ändring i x (dvs. d x) kommer det att finnas en f ⁽¹⁾ (x <) d x ändring i f. Använda gränser man kan sluta med den här definitionen enligt följande. Antag att Δ

x är förändringen i x i en godtycklig punkt x och Δ f är motsvarande ändring i funktionen f. Det kan visas att Δ f = f (1) ⁽ x) A x + e, där e är felet. Nu är gränsen Δ x → 0 Δ ^{f /} Δ _{x =} f (1) ( ^x ) (med den tidigare angivna definitionen av derivat) och sålunda, A x → 0 e / ^A x = 0.Därför är det möjligt att dra slutsatsen att Δ _{x → 0} ε = 0. Nu betecknar Δ x → 0Δ f som d f och Δ x → 0A x som d x erhålls definitionen av differentialen noggrant. Till exempel är skillnaden mellan funktionen. Vid funktioner av två eller flera variabler definieras den totala differensen av en funktion som summan av skillnader i riktningarna för var och en av de oberoende variablerna. Matematiskt kan det anges som

Vad är skillnaden mellan derivat och differential?

• Derivat avser en förändringshastighet för en funktion medan skillnaden avser den faktiska ändringen av funktionen, när den oberoende variabeln utsätts för förändring.

• Derivatet ges av

, men skillnaden ges av

Skillnad mellan derivat och differential

Rekommenderad